앞선 시간에 학습 알고리즘은 인간의 사고 과정을 그대로 따라 간다고 말했습니다.
.
만약 사람이 어떤 데이터를 토대로 결과를 예측했는데 틀렸다면 무엇이 틀렸는지 확인하고 결과가 올바르게 나타나는 방향으로 수정할 것이고
머신 러닝을 예측의 틀린 정도를 오차(Error)로 생각하고 올바른 결과가 나오도록 방정식을 수정하는 것입니다.
.
오차를 수정하는 방식에는
최소제곱법(method of least squares — LSM or LMS) 최우추정법(maximum likelihood method — MLE) 최대사후확률추정(maximum a posterior estimation — MAP) 기울기(미분) 강하법(gradient descent — GD)
등등이 있고
.
오늘은 이 오차를 수정하는 방식에 대해 말해보겠습니다.
.
Andrew ng 교수님의 명강의
.
매우 많은 머신러닝 강좌들이 있는데 대부분이 Cost Function과 Gradient Descent 만을 언급하고 넘어가버립니다.
.
가장 쉽게 접근할 수 있고 적어도 local minimum을 찾는다는 보장이 있기 때문에(수학적으로 증명되어있습니다) GD를 선호하기 때문입니다.
.
그렇다면 백문이 불여일견!
위에 언급한 기본적인 4가지 방식에 대해 설명하겠습니다.
.
1. 최소제곱법(LSM or LMS)
실제 답과 결과 값의 오차의 제곱의 합이 최소가 되는 해를 구하는 방법
.
머신러닝에서 배우는 가장 단순한 모델로 입력과 출력의 관계가 선형이라고 가정합니다.
.
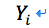
알고 싶은 값
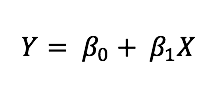
예측 방정식
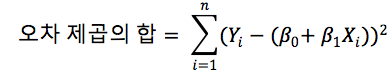
예측과 알고 싶은 값의 차이(유클리드 거리)의 제곱
>> 오차의 제곱의 합은 위와 같이 표현되며 이 값을 최소값을 구하기 위해서
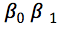
최적화 해야하는 변수
에 대해서 각각 편미분한 값이 0 이되도록 하는 점을 찾는 것 이겠지요.
그러면
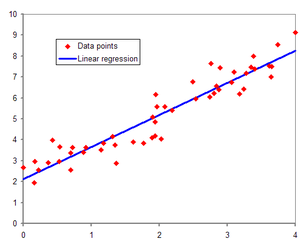
Linear Regression — wikipedia
위와 같이 데이터들이 있을 때 오차의 제곱이 제일 작은(값들을 깔끔하게 통과하는) 함수를 얻을 수 있는 것입니다.
.
이 방법은 간단한 계산이지만
데이터가 많아지면 계산량이 매우 많이 증가한다는 단점이 있습니다.
.
이때 오차 제곱의 합을 Cost Function이라고 하고 이는 나중에 Gradient Descent에서도 사용하게 됩니다.
이번에는 확률의 개념을 생각해보겠습니다.
.
2. 최우추정법(MLE)
— 위키피디아에서는 (최대가능도 방법) 이라고 하는 군요
원하는 결과가 나올 가능성을 최대로 만드는 모수를 선택하는 방법
.
말이 참 어렵네요.
쉬운 예제로 설명을 해보자면
동전 던지기를 한다고 생각해보는 겁니다.
.
10번 던져서 앞앞앞앞앞뒤뒤뒤뒤뒤(원하는 결과) 가 나왔다고 하면
동전 던지기라는 행위는 1/2 확률(모수)이라고 생각할 수 있습니다.
.
그런데 만약 10번 다 앞면만 나왔다면???
정말 극한의 확률이 나왔을 수도 있지만
동전 던지기라는 행위가 1/2 확률이 아니라 다를 것이라고 생각하는 것입니다. (가정입니다.)
그래서 10번 다 앞면이 나오려면 동전 던지기의 확률이 어떨 때 가능성이 제일 높을까?를 구하는 것입니다.
(결과를 보고 원인을 추측하는 것이지요)
.
이를 가능도(likelihood)라고 합니다.
.
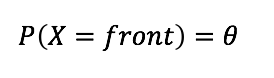
동전 던지기 앞면의 확률
동전 던지기 앞면의 확률을 P(x = front) = theta라고 하면
.
10번 다 앞면이 나온 가능도는
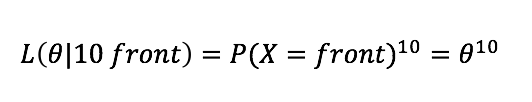
10번 다 앞면이 나오는 가능도
이라고 할 수 있습니다.
당연히 미분해볼 필요도 없이 최대값은 P(x) = 1 이겠네요.
.
7번 앞면, 3번 뒷면이라고 하면
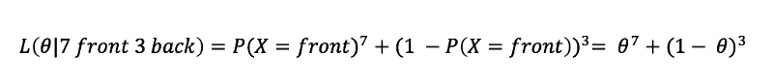
7번 앞면 3번 뒷면 나오는 가능도
이라고 할 수 있을 것이고
.
미분하여 계산하면 최대값을 구할수 있고 계산이 매우 귀찮을 것이므로 보통 로그를 취해서 계산합니다.(단조 증가이므로 경향 변하지 않음)
.
이 부분에 대한 자세한 내용은 매우 매우 수학적인 이야기이므로 링크로 첨부하겠습니다.(읽어보시기를 추천합니다.)
.
최대가능도 방법
https://ko.wikipedia.org/wiki/최대가능도_방법
계산에 대한 이야기
https://medium.com/@youngji/최대-가능도-방법-maximum-likelihood-method-a8546e44c1a3#.nlocgibz9
.
위 링크의 글을 읽어보신 분에게 한가지 더 이야기 할 것이 있습니다.
처음 언급한 LSE와 MLE와의 관계에 대한 것입니다.
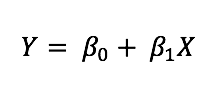
LSE에서 본듯한 수식
LSE는 데이터들과 오차가 가장 적은 선형해를 구하는 것인데
만약 데이터들이 표준정규분포(white gaussian noise)로 나타난다면
데이터들은
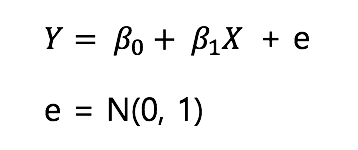
표준 정규 분포를 따르는 데이터들
이와 같이 나타날 것이고
이를 MLE를 사용 해보면
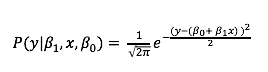
주어진 식을 만족할 확률
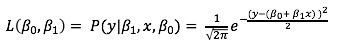
가능도
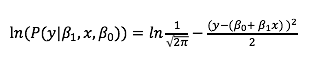
로그를 취해본다.
로그를 취한 결과를 보면 결국
이전에 LSM의 오차가 최소가 되는 조건이
MLE의 가능도가 최대가 되는 것이라는 것을 알 수 있습니다.
.
결국 LSM은 MLE에 포함되는 개념이며
Likelihood라는 척도로 최적화를 진행하는 것입니다.
.
.
그런데 이 방법은 큰 문제가 존재합니다.
위에 동전을 던질때 10번 다 앞면이 나왔다면
이 동전은 100%확률로 앞면이 나오는 것일까요?
.
아닙니다.
.
데이터의 수가 무수히 많아서 모든 경우를 고려하지 않는다면 이 방법은 편협한 확률게임을 할 수 있습니다.
그래서 최대사후확률추정(MAP)이 등장합니다.
.
continue…..
2부 링크
https://medium.com/mathpresso/mathpresso-머신-러닝-스터디-3-5-오차를-다루는-방법-2-e23e08d95cc3#.5jun95b49
cf) 오탈자 혹은 잘못된 개념에 대한 피드백은 항상 환영합니다.