3. 최대사후확률추정(MAP)
최우추정법과 같이 모수(parameter)의 추정에 사용하지만
.
최우추정법에서는 원하는 결과가 일어날 확률을 최대로 만드는 parameter를 찾는 것에 비해
최대사후확률추정은 parameter에 확률 분포를 주어서 베이즈 정리를 이용해 결과를 최대로 하는 값을 찾는 것입니다.
.
B 사건이 일어났을 때 A가 일어날 확률을 조건부 확률이라 하며
P(A|B)
로 표현합니다.
.
이는 베이즈 정리에 따르면
P(A|B) = P(B|A)*P(A)/P(B)
입니다.
결론 : A > B 확률을 통해서 B > A 확률을 추측할 수 있는 것입니다.
.
동전던지기로 알아볼까요?
마찬가지로 10번의 동전을 던졌는데 8번 앞면만 나왔다고 했을 때
A : 동전던지기의 확률(0.5)
B : 결과의 확률(0.8)
P(A|B) — 결과가 나왔을 때 동전던지기의 확률
P(A|B)
= P(B|A)*P(A)/P(B)
= 동전던지기로 10번 던졌을 때 8번 나올 확률 * 동전던지기의 확률 / 결과 값의 확률 = (10C8*(1/2)⊃1;⁰* 1/2) / (0.8)
.
지금 우리는 알고 싶은 값 x 를 0.5로 고정해놓고 계산하는 것이고
이를 x 로 놓으면
.
P(x|0.8) = P(0.8|x)*P(x)/P(0.8)
우변의 식은 x에 대한 함수로 표현될 것이고 최대값을 구할 수 있을 것입니다.
그 과정이 바로 최대사후확률추정(MAP)입니다.
.
이 방법은 초기에 사전 지식을 주입해서 원하는 방향으로 답을 이끌어갑니다. (인간이 가진 생각, 직관을 반영하는 것이지요)
.
이런 방법은 data를 얻기 힘든 경우에 효과를 발휘합니다.
.
최우추정법(MLE)가 과적합(overfitting)과 노이즈에 취약하기 때문에 이것을 사전 지식으로 보정한다고 생각할 수 있습니다.
.
그러나 그 직관이 잘못된 것이라면 매우 안좋은 모델이 될 수 있습니다.
초기값 설정이 중요한 것이지요!
.
이제 많은 강의에서 숱하게 언급하는 Gradient Descent 입니다.
.
4. 기울기(미분) 강하법(GD)
함수의 기울기를 구하여 기울기가 낮은 쪽으로 계속 이동시켜서 극값에 이를 때까지 반복하는 것
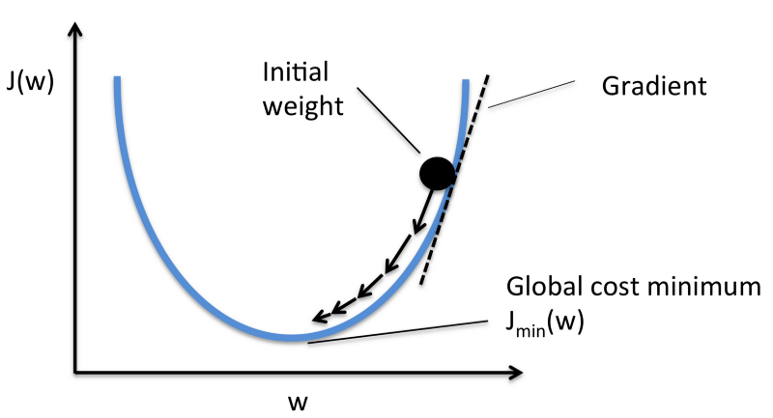
출처 : http://sebastianraschka.com/faq/docs/closed-form-vs-gd.html
2차원에서 한번 볼까요? 이와 같은 2차 방정식을 미분하여 그 경사를 따라서 움직이고 이를 반복하면 최소값으로 수렴합니다.
이 그래프를 오차의 그래프라고 하면 Cost Function 일 것이고
이를 최소화 하는 방법이 Gradient Descent 입니다.
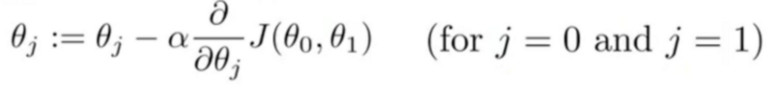
gradient descent — Coursera Machine Learning Taught by: Andrew Ng
.
미분한 값으로 값을 갱신하여 최소값으로 수렴합니다.
아까 설명한 최소제곱법이랑 결과도 같고 계산도 최소제곱법이 편하지 않나요???? 하고 생각하실수 있습니다.
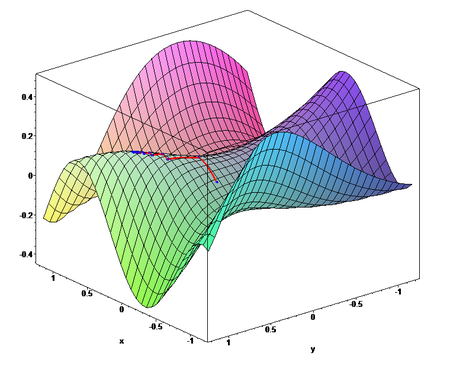
gradient descent — wikipedia
그런데 함수가 Quadratic function이 아니라면 미분해서 한번에 에러가 최소가 되는 지점을 계산하는 것은 매우 어렵습니다.
(Quadratic function — https://en.wikipedia.org/wiki/Quadratic_function)
.
그렇기에 예시에서 처럼 오차가 줄어드는 방향으로 기울기 하강을 선택하는 것입니다.
.
이렇게 하강한다면 언젠가는 최소값으로 도달할 것이고 우리는 오차의 최소값을 얻을 수 있습니다.
(물론 학습률에 따른 기울기 발산, 너무 느린 학습 속도, 지역 최소값(local minimum)등등 문제가 있는 엄청 허술한 결론이지만 이를 보완하는 많은 응용이 존재합니다.)
.
.
그렇다면 오차를 다루는 최적화 방법은 정말 GD만 알고 넘어가면 될까요??
.
실제 머신러닝 연구분야에서는 최적화 방법을 훨씬 다양하게 접근하고 있다고 합니다.
.
Neural Network과 같이 생물 유전학에서 착안하고 다윈의 적자생존 이론을 기본 개념으로 하는 유전알고리즘(Genetic Algorithm)과
.
재료 공학의 풀림(annealing)에서 착안하여 에너지 관점으로 최적점을 찾아가는 Simulated annealing 방식을 생각해볼 수 있습니다.
.
이 두 가지 방식은 미분을 구하지 않고 최적화를 하는 방식이지만 local minimum을 찾는다는 수학적인 증명이 아직 없어서 연구가 진행되고 있는 분야라고 합니다.(다른 참신한 방법도 계속 나오고 있겠지요??!!)
.
이상으로 오차의 수정에 대한 간단한 개론을 하고 후에 어떠한 응용들이 존재하는지 알고리즘과 함께 알아보겠습니다.
다음 시간에는 회귀 분석(Regression) 주제로 돌아오겠습니다.
.
cf) 오탈자 혹은 잘못된 개념에 대한 피드백은 항상 환영합니다.
2016.11.17 1차 수정 — 피드백 주셔서 정말 감사합니다!