길었던 서론을 뒤로하고 실제 알고리즘으로 들어가보도록 하겠습니다.
.
회귀 분석 (Regression)
.
회귀 분석은 주어진 데이터가 어떤 함수로부터 생성됐는가를 알아보는 ‘함수 관계’를 추측하는 것 입니다.
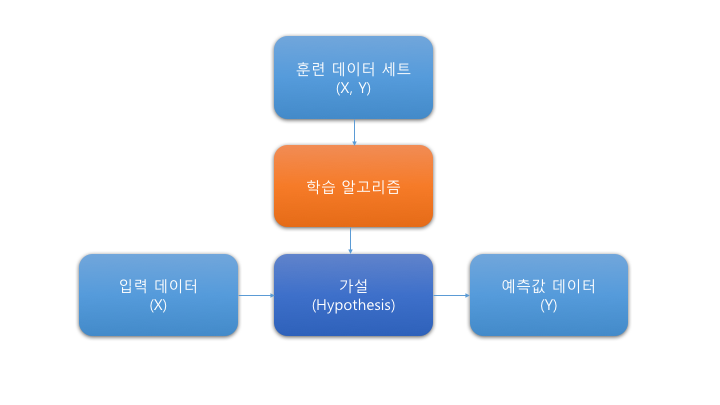
머신러닝 개념도
가설(방정식이) 몇차 방정식인지? 그리고 계수는 각각 무엇인지 알아보는 것입니다.
.
이 방정식의 계수가 선형이면
선형 회귀 분석(Linear Regression Analysis)
.
그 중에서도 방정식의 변수가 여러개 이면
다중 선형 회귀 분석(Multiple Linear Regression Analysis)
이라고 합니다.
.
한번 테스트 데이터로 알아보도록 하겠습니다.
(앞으로 나오는 모든 데이터 및 결과는 아래 링크에서 확인하실수 있습니다. 부분 부분 마다 한글 주석을 첨부했습니다.)
(LinearRegression.py, MultivariableLinearRegression.py > setting: python 3.5, tensorflow)
proauto/ML_Practice Contribute to ML_Practice development by creating an account on GitHub.github.com
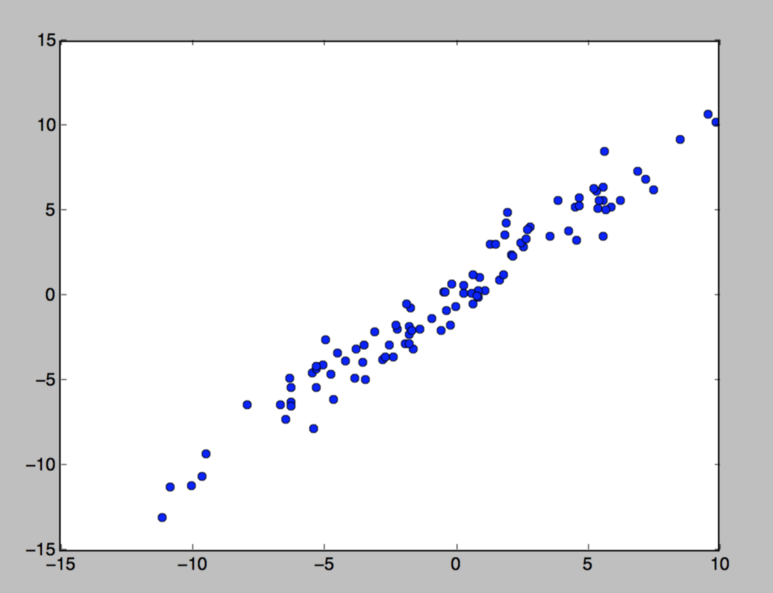
선형 회귀 분석 — 테스트 데이터(LinearRegression.py)
이 데이터를 가장 알맞게 표현하는 함수는 무엇일까요??
.
결과 부터 말하자면 이 것은
y=x 그래프에 약간의 오차를 섞어 만든 데이터 입니다.
그렇다면 한번 학습을 해보겠습니다.
.
y = w*x + b (초기값 - w : -1~1 랜덤, b = 0)
이라고 정의하고 결과값과의 오차(error)를 Gradient Descent를 사용해서 학습해보겠습니다.
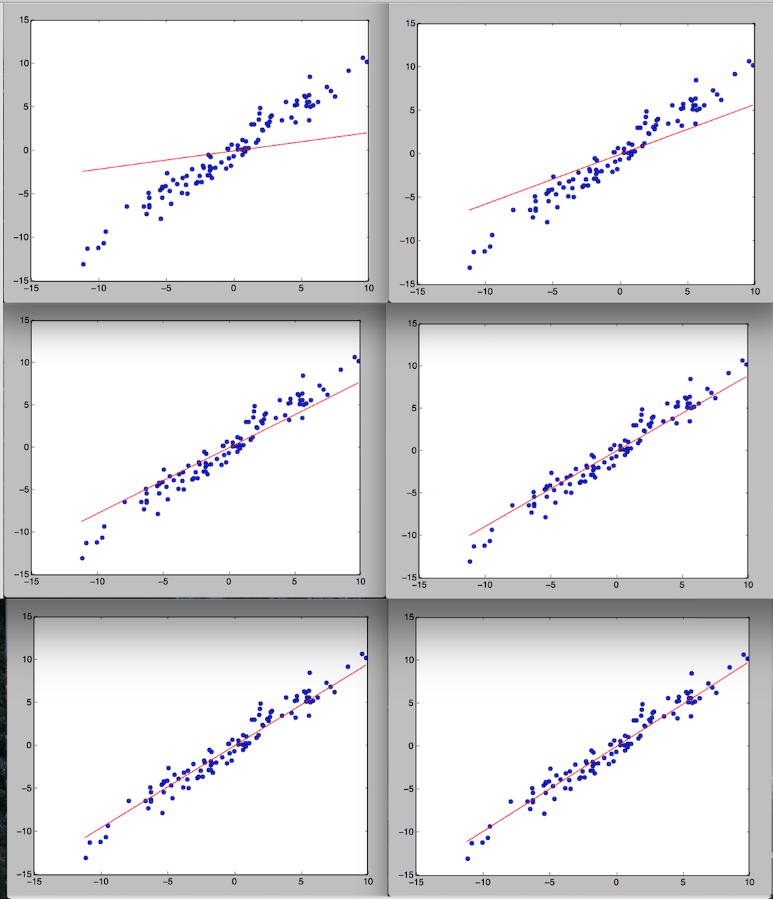
학습 결과(LinearRegression.py)
학습 결과는 왼쪽 위부터 오른쪽 아래 방향입니다.
.
처음에는 y = 0.3*x 정도의 함수를 랜덤으로 설정한 것으로 보여지는데
학습을 진행할 수록 y = x 그래프에 가까워지는 것을 확인할 수 있습니다.
.
.
이번에는 x1, x2 두가지 변수를 갖는 다중 회귀 분석을 살펴보겠습니다.
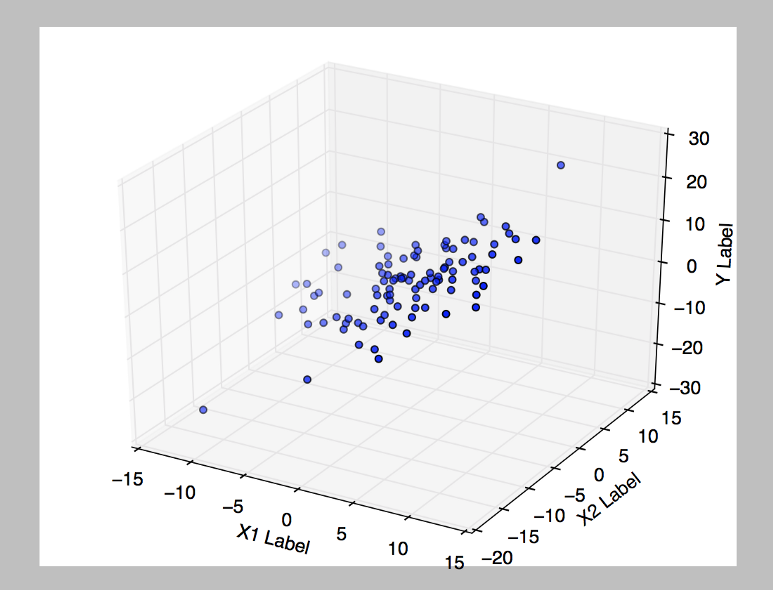
테스트 — 다중 회귀 분석(MultivariableLinearRegression.py)
위와 같은 데이터가 주어졌을 때
(y = x1 + x2 그래프에 오차가 추가된 데이터)
.
y = w1 * x1 + w2 * x2 + b(초기값 — w1, w2 : -1~1 랜덤, b = 0)
라고 정의하고 학습을 해보면 아래와 같은 결과를 얻을 수 있습니다.
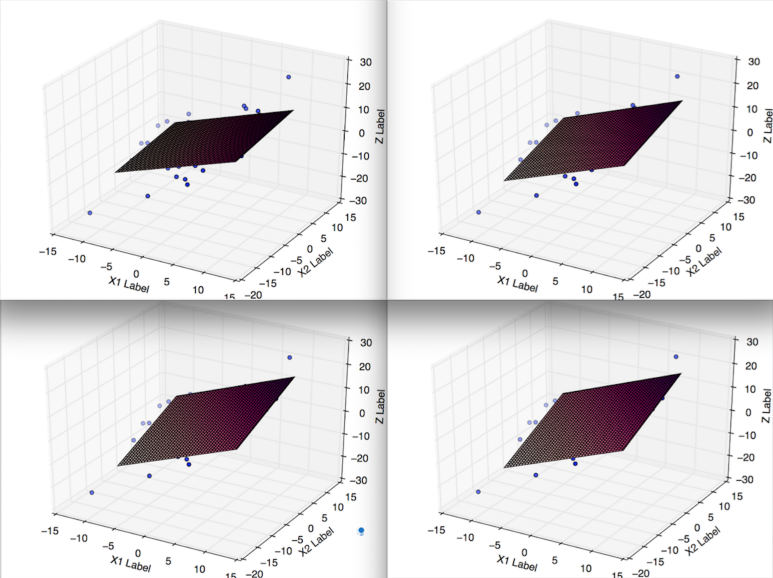
다중 회귀 분석의 결과(MultivariableLinearRegression.py)
변수가 2개 이기 때문에 결과는 평면으로 나타내고 학습을 진행할수록 오차가 작아지는 평면을 결과로 얻습니다.
.
이렇게 단일, 다중 회귀 분석을 통해서 우리는
데이터가 존재하면
그 데이터를 표현하는 함수를 학습할 수 있음을 확인했습니다.
.
이를 이용하면 과거의 데이터를 통해서 미래의 데이터가 어떠할지 예측할 수 있습니다.
단일 회귀 분석에서 x축이 시간이라면 내일의 y 값을 예측할 수 있겠지요?
.
이번에는 간단히 선형 회귀 분석에 대해서 알아보고
다음에는 로지스틱 회귀와 변수의 개수 혹은 차수를 결정하는 방법에 대해서 이야기 하겠습니다.
.
cf) 오탈자 혹은 잘못된 개념에 대한 피드백은 항상 환영합니다.
Enter가 안먹히는걸 이제 알았네요… 마침표로 대체합니다.