2부 — 그래서 어떻게 쓰면되지?
.
이제 실제로 인공신경망을 문제 해결에 사용해 보겠습니다.
.
이 것은 지난 시간에 시스템 모델링 했던 뉴런 모델입니다.
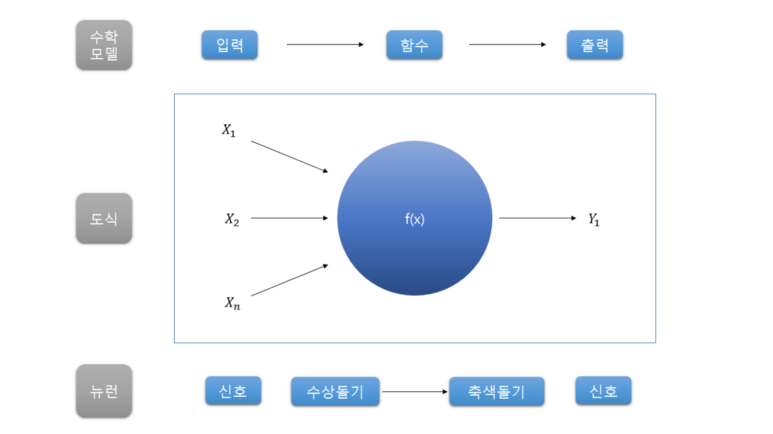
Neuron을 시스템 모델링 한 것
.
위와 같은 모델은 수학적으로 표현하고 다시 그려보면
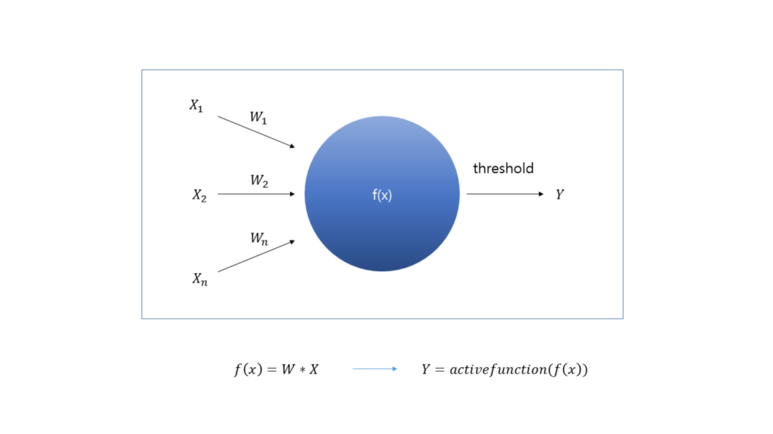
뉴런의 수학적 표현
위와 같이 표현할 수 있습니다.
.
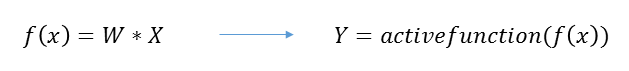
수학적 표현 확대
뉴런의 수학적 표현
입력값들(X)에 가중치를 두어(W) 값(f(x))을 구하고 그 값과 임계치와의 관계를 활성함수(active function)로 판단하여 결과값을 출력하는 것입니다.
.
이때 활성함수는 뉴런에서 임계값을 넘었을 때만 출력하는 부분을 표현한 것으로 다양한 방법이 있습니다.
.
step 함수 — 임계값 넘으면 1
sigmoid 함수 — 임계값 기준으로 S 자 형태
Relu 함수 — 임계값 이하는 0, 임계값 넘으면 선형 증가
등등 많은 방식이 있습니다.
.
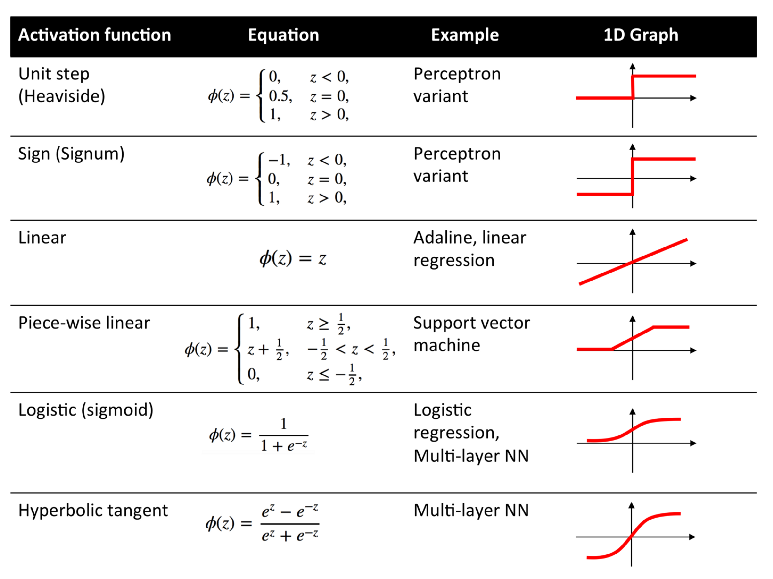
https://www.quora.com/What-is-the-role-of-the-activation-function-in-a-neural-network
hunkim.github.io/ml/ > Vanishing Gradient 를 위해 Sigmoid 보단 ReLu를 사용합니다.
.
이런 활성 함수들의 성능 또한 매우 다양합니다.
어떤 활성 함수를 쓰느냐에 따라서 학습 속도나 정확도가 달라집니다.
(논문들 중에는 다양한 활성 함수를 사용해보면서 성능 변화를 관측하는 것들도 있습니다.)
.
그러면 오늘 예제는 이전에 했었던 MNIST 사진 분류를 재활용 해보겠습니다.

참 좋은 예제 MNIST
.
이전 예제들에서 로지스틱 회귀와 KNN 방식으로 학습을 했었는데
오늘은 DNN(Deep Neural Network)으로 한번 해보겠습니다.
.
은닉층이 2개인 DNN을 이용해서 학습을 해보니
(활성 함수 — ReLu, 분류 방식 — softmax)
95% 정도의 정확도를 나타내는 것을 보입니다.
.
( MNIST_MultipleLayerPerceptron.py
> setting: python 3.5, tensorflow,numpy)
proauto/ML_Practice ML_Practice -Python(with Tensorflow)github.com
.
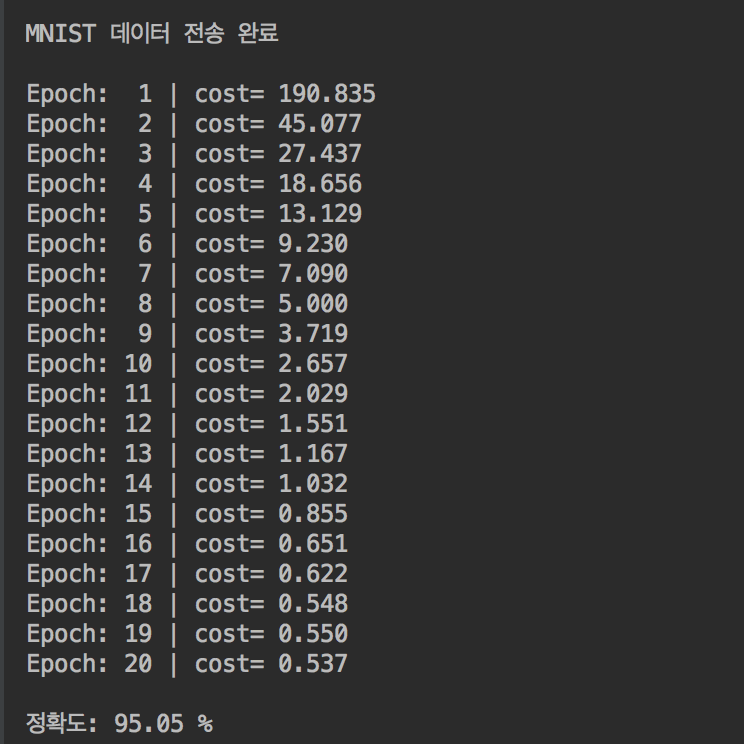
학습 과정과 결과
.
물론 로지스틱 회귀를 했을 때보다 시간이 훨씬 많이 걸리기는 하지만
성능은 매우 우수한 것을 볼 수 있습니다.
.
개념은 매우 복잡해졌지만 코드 상으로 단순 로지스틱 회귀보다 크게 길어지지도 어려워지지도 않았습니다.
.
또한 은닉층 개수를 많이 늘릴 수 있는 컴퓨터 환경이 구축되어서 인공신경망 분야는 매우 각광받게됩니다.
.
DNN(Deep Neural Network), CNN(Convolution Neural Network), RNN(Recurrent Neural Network), Deep Q-Networks 등등 기존의 한계 극복 혹은 새로운 방식으로 발전하고 있습니다.
(이제 인공신경망이라는 단어보다는 딥러닝(Deep Learning)이라는 단어를 선호하는 듯 합니다.)
.
새로운 방식들을 소개하고 싶지만 하나하나 매우 광범위한 내용을 포함하기에 훗날을 기약하고
.
다음 시간에 비지도학습 — 군집화(Clustering) 를 주제로 돌아오겠습니다.
.
cf) 오탈자 혹은 잘못된 개념에 대한 피드백은 항상 환영합니다.
머신러닝 추천 강의 & ReLu 사진 출처
hunkim.github.io/ml/