오늘부터는 기존의 스터디에 추가적으로 진행하는 보충(?) 스터디를 진행하겠습니다.
.
첫번째 주제는
밀도 추정(Density Estimation)
입니다.
.
주의 : 수식을 배제하고 설명하려고 노력했습니다. 자세한 수식이 궁금하신 분들은 아래의 참고 자료를 확인해주세요!
.
밀도 추정은 통계학에서 다루는 용어로 데이터와 변수의 관계를 파악하는 방법입니다.
.
간단한 예시를 들어서 설명을 진행해보겠습니다.

얼마전에 수능이 끝났습니다!!
.
우리의 목표를 학생이 수능 시험을 봤을 때 어떤 성적을 받을지 예측하는 것으로 해봅니다.
.
변수는 (모의) 수능 시험 성적입니다.
.
그리고 데이터는 실제로 변수에서 관측된 값이지요. (0점 ~ 400점)
.
우리는 모의 수능 시험 성적(데이터들)을 토대로 수능 시험 성적(변수)가 얼마가 나올지 예측할 수 있습니다.
.
이제 다시 한번! 그리고 구체적으로 말하면
밀도 추정은 데이터로 부터 변수가 가질 수 있는 모든 값의 밀도(확률)을 추정하는 것이지요.
.
학생이 평소 받아왔던 성적과 비슷한 성적을 받을 것이라는 것을 확률적으로 표현한 것입니다.
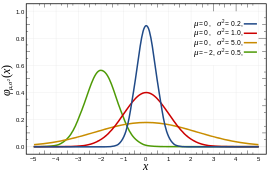
이런 식으로 그림을 그릴 수도 있겠지요?? — wikipedia
.
이때 고민을 하게 되는 부분은 저렇게 깔끔하게 분포가 나타날까? 입니다.
.
위 그림은 정규 분포(Gaussian distribution)를 따르기 때문에 좌우 대칭으로 아주 예쁜 그래프가 나오지만 보통의 데이터들은 아닌 경우가 많습니다.
.
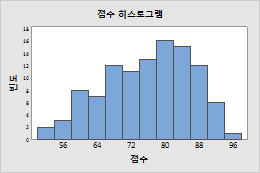
성적 히스토그램 — http://support.minitab.com/ko-kr/minitab/17/topic-library/basic-statistics-and-graphs/graphs/graphs-of-distributions/histograms/create-a-histogram-with-frequency-data/
.
이런 식으로 점수가 나올 수도 있겠지요?
.
이런 분포는 미리 확률 밀도에 대한 함수를 정해두고 가중치(weight)를 학습하는 방식으로는 어렵습니다. (Supervised Learning)
.
그렇기에 우리는 사전 지식 없이 데이터를 통해서 확률 밀도 함수를 추정하는 것입니다. (Unsupervised Learning)
.
가장 쉽게 사용할 수 있는 것은 위와 같은 히스토그램에 의해 추정을 하는 것입니다.
.
이 방법이 간단하긴 하지만 히스토그램의 discrete한 데이터는 관측 step 경계에서 불연속적이며 관측 step 크기에 따라 관측 시작점이 달라지고 분포가 다른 의미를 갖기에 문제가 있습니다.
또 고차원의 데이터에서는 관측 step도 기하급수적으로 증가하고 메모리 문제가 생긴다고 합니다.
.
.
이러한 문제를 해결하기 위한 방법이
KDE(Kernel Density Estimation — 커널 밀도 추정)
입니다.
.
커널 밀도 추정은 커널 함수라는 것을 사용합니다.
.
커널 함수(Kernel)는 원점을 중심으로 대칭이며 적분값이 1 인 양의 함수로 정의할 수 있습니다
> 확률 분포를 나타내기에 적합한 함수
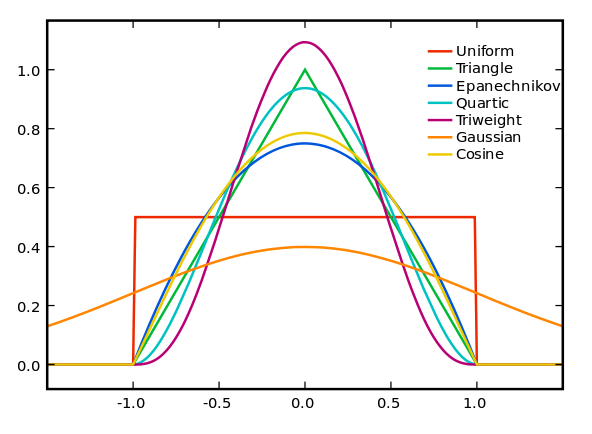
다양한 커널 함수들 — https://en.wikipedia.org/wiki/Kernel_(statistics)
.
다양한 친구들이 있는데 KDE는 이들을 사용하여 주어진 데이터의 분포를 반영하는 새로운 분포를 만드는 것입니다.
.
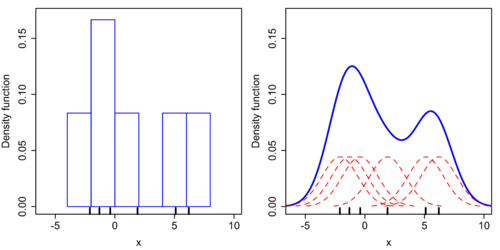
히스토그램과 Gaussian 분포를 이용한 커널 밀도 추정 — https://en.wikipedia.org/wiki/Kernel_density_estimation
.
왼쪽과 같은 분포가 있다고 할 때 Gaussian 분포를 커널 함수로 사용하면 오른쪽과 같이 밀도 추정을 얻을 수 있습니다.
.
오른쪽 그래프는 왼쪽의 히스토그램을 Smoothing 하여 Continuous한 그래프로 바꾸었다고 생각할 수 있습니다.
.
이것으로 인해 매끄러운 그래프를 얻기는 했지만 고차원이 되었을 때의 문제에서는 여전히 자유롭지 못합니다.
.
.
그래서 생각해 낸 것이
K-최근접 이웃 추정(K-Nearest Neighbors Estimation)
입니다.
.
KNN(K-Nearest Neighbors)를 앞서 살펴 보았었는데 매우 비슷하게 작동합니다.
.
인접한 K개의 점을 찾는 것은 같으나 그것이 포함되는 영역의 크기에 따라서 확률 밀도를 나타내는 것입니다.
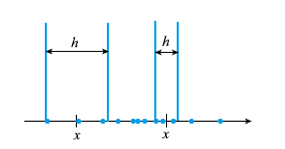
서적 : 패턴인식 — 오일석님
.
이렇게 x라는 점을 기준으로 2개의 최근접 점을 찾을 때
영역의 너비 h가 넓으면 확률이 작은 것으로
너비 h가 넓으면 확률이 큰 것으로 인식할 수 있습니다.
(데이터의 밀도라는 개념이 어느 정도 들어 맞습니다.)
.
이러한 방법들을 통해서 우리는
사전 지식 없이 데이터 만으로 그 데이터들이 어떤 분포로 나타날지 알 수 있습니다. (Unsupervised Learning)
.
다음 시간에는 또 하나의 비지도 학습 방법인 차원 축소(Dimension Reduction)로 돌아오겠습니다.
.
cf) 오탈자 혹은 잘못된 개념에 대한 피드백은 항상 환영합니다.
.
참고 싸이트
http://darkpgmr.tistory.com/147
https://en.wikipedia.org/wiki/Kernel_density_estimation
jun.hansung.ac.kr/PR/10 Non-parametric Density Estimation.ppt
http://johngiraffe.tistory.com/7