오늘은
차원축소(Dimensionality Reduction)
에 대한 이야기를 해보겠습니다.
.
오늘은 선형대수의 내용이 많이 포함되어 있지만 수식 관련된 부분은 모두 링크로 대체합니다.
(이게 어디 쓰는 거지? 하는 의미를 전달하기 위한 스터디 입니다 ㅎㅎ)
.
.
본격적인 이야기에 앞서
왜 차원 축소를 하는 거지? 에 대해 생각해보겠습니다.
.
지난 시간에 밀도 추정에 대한 이야기를 하면서 고차원이 되었을 때의 문제에 대해서 언급했습니다.
고차원의 데이터에서는 관측 step도 기하급수적으로 증가하고 메모리 문제가 생긴다고 합니다.
이렇게 어려운 말로 써놨었는데….
.
이를
차원의 저주(Curse of dimensionality)
라고 합니다.
.
차원이 증가하면 그것을 표현하기 위한 데이터 양이 기하급수적으로 증가한다는 것입니다.
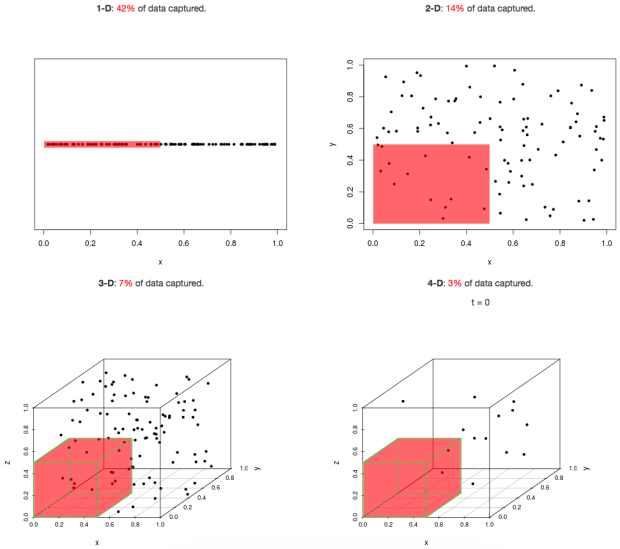
데이터가 차원의 증가에 따라 얼마나 많이 필요할 지를 나타냅니다.
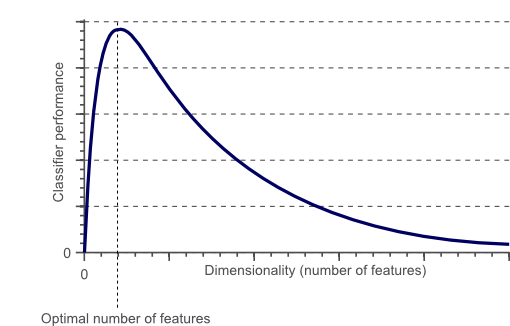
일정 차원을 넘으면 분류기의 성능은 점점 떨어져 0으로 수렴
차원의 저주 시각화 : http://freesearch.pe.kr/archives/3211
.
그렇기 때문에 너무 고차원의 데이터들은 의미를 제대로 표현하기 어렵습니다.
.
이러한 데이터들을 우리는 차원 축소를 하여 다룹니다.
.
차원 축소(Dimensionality Reduction)
데이터의 의미를 제대로 표현하는 특징을 추려내는 것
.
대부분의 상황에서 차원의 크기는 특징의 개수를 나타내고
특징(feature)이 너무 많기 때문에 학습이 어렵고 더 좋은 특징만 가지고 사용하겠다는 것입니다.
.
그렇다면 이러한 특징은 어떻게 뽑아낼까요?
.
여러가지 방식이 있지만 기본적인
주성분분석(PCA — Principal Component Analysis)
을 살펴보겠습니다.
.
주성분분석은 데이터의 분포를 가장 잘 표현하는 성분을 찾아주는 것입니다.
.
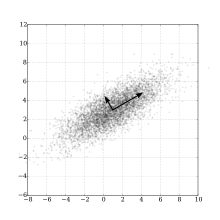
데이터 분포와 그들의 주성분 — Wikipedia
.
위의 그림에서 x, y 축보다 화살표방향의 두 축이 이 데이터를 더 잘 표현하는 것(주성분)을 알 수 있습니다.
.
주성분은 통계학적으로 데이터들의 분산이 가장 큰 방향 벡터를 말합니다.
(분산 - 데이터가 평균에서 얼마나 떨어져 있는가를 의미)
.
주성분을 찾아내는 방법은 매우 잘 설명되어있는 블로그로 연결하겠습니다.
PCA (Principal Component Analysis), 주성분 분석 PCA는 고차원(ex: (x 1,···x 10))의 데이터를 저차원 (ex: (x 1x 2x 3))으로 압축하는 대표적인 차원 축소( dimension reduction ) 방법입니다. 예를 들어 10차원의 데이…t-robotics.blogspot.kr
.
이어서 PCA의 한계도 소개가 되어있습니다.(바로 뒤통수.. ㅎㅎ)
PCA(주성분분석)의 의미와 한계점 데이터가 고차원일 때 차원축소( dimensionality reduction ) 방법은 데이터를 분석하고 시각화(visualize) 하는데 매우 편리한 수단을 제공합니다. 사실 우리가 관측한 데이터는 관측된 차원…t-robotics.blogspot.kr
.
그러면 이제 우리의 스터디 목적인!
머신러닝에서 차원 축소를 어떻게 사용할까요?
.
이미 한번 사용했었는데 CNN의 Pooling(Subsampling)도 차원 축소의 한 방법입니다.
.
너무 많은 Feature가 있기 때문에 학습의 어려움이 있어서 줄였던 것입니다.
.
이렇게 차원 축소는 학습의 Preprocessing 단계에서 데이터를 학습하기 좋은 형태로 다듬는 역할을 합니다.

차원 축소 ≈세공
.
막무가내 데이터를 학습하는 것보다 매우 큰 효과를 발휘하게 때문에 복잡한 모델 학습을 위해서는 꼭 알아두어야 할 것 같습니다.
.
이상으로 차원 축소에 대한 스터디를 마치고 다음 시간에는 TensorFlow를 주제로 정리하는 시간을 갖겠습니다.
.
cf) 오탈자 혹은 잘못된 개념에 대한 피드백은 항상 환영합니다.
참고 싸이트
https://en.wikipedia.org/wiki/Dimensionality_reduction
http://sanghyukchun.github.io/72/
http://darkpgmr.tistory.com/110
http://t-robotics.blogspot.kr/2014/10/pca-principal-component-analysis.html#.WDbNtBKLRTY
http://t-robotics.blogspot.kr/2015/12/pca.html#.WDfRzBKLRTZ
http://terryum.io/korean/2016/05/05/FeatureSelection_KOR/
PCA 이해에 대한 후기(수학적인 의미에 대한 고민이 담김)
http://gentlej90.tistory.com/15
사진 출처
http://www.newsnshit.com/curse-of-dimensionality-interactive-demo/
http://www.visiondummy.com/2014/04/curse-dimensionality-affect-classification/