
#3에서는 선형 회귀(Linear regression)에 관하여 알아보려고 합니다.
선형회귀는 크게 두가지로 분류 될 수 있습니다.
1) 단순 선형 회귀(Simple linear regression)
단순 선형 회귀는 하나의 스칼라 독립 변수(x)와 하나의 스칼라 의존 변수(y) 사이의 선형 관계를 나타냅니다.
2) 다중 선형 회귀(Multiple linear regression)
다중 선형 회귀는 둘 이상의 스칼라 독립 변수(x)와 하나의 스칼라 의존 변수(y) 사이의 선형 관계를 나타냅니다.
그럼 선형 회귀 분석을 먼저 수학적으로 알아 보도록 하겠습니다.
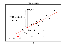
우리가 독립 변수(x)와 의존 변수(y)를 여러개 가지고 있을 때(데이터 셋을 가지고 있을 때), 위에 그림과 같은 데이터 분포도를 그릴 수 있습니다. 이 데이터 셋으로 우리는 회귀선(Regression line)을 그릴 수 있고, 이 회귀선을 통해 어떤 독립변수(x)에 대한 의존 변수(y)의 추정값을 도출해 낼 수 있습니다. 이 추정값을 우린 y-hat으로 표현합니다. 여기서 b0는 절편이며 표본회귀상수라고 부르고 b1은 기울기이며 표본회귀계수라고 부릅니다.
그럼 회귀선을 어떻게 그릴 수 있을까요?
최소제곱법(Least sqaure)을 이용하여 풀어보도록 하겠습니다.
먼저 회귀선(Best fitting line)을 만들기 위해 목적함수(우리가 최소화하거나 최대화해야하는 목적이 되는 함수)를 세워 봅시다.

잔차의 제곱합을 최소화하는 라인을 그리면 회귀선이 됩니다.

이 함수를 Minimize 하기 위한 조건으로, Objective function을 각각 b0와 b1으로 편미분한 값이 0을 만족해야합니다.

Objective function을 b0로 편미분한 식입니다.

b0와 b1은 상수 취급을 받으니 시그마에서 앞으로 빼줍니다.
위 식에서 전체 식을 n으로 나눠 주면 yi에 대한 식은 y의 평균(y_bar)가 되고, xi에 대한 식은 x의 평균(x_bar)가 되므로 정리하면 아래와 같은 식이 됩니다.

그러면 이번엔 b1에 대해 편미분 해봅시다.
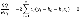
Objective function을 b1에 대해 편미분한 식입니다. 여기서 양변에 -2를 나눠줍시다.

-2로 나눠준 식을 전개하면 빨간 식이 나옵니다.
이제 위에 빨간색으로 칠해져 있는 두 식을 이용해보도록 하겠습니다.
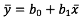
이 식을 x_bar의 항을 이항하여 b0에 대한 식으로 바꿔주고,

이 식의 b0 자리에 대입해주면 됩니다.
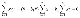
아래 x의 평균에 대한 식으로 위에 식을, b1이 포함된 항은 b1으로 묶일 수 있도록 바꿔줍니다.

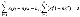
이제 b1항을 이항하고 나눠주면 b1에 대한 식이 나옵니다.

나온 식에서 x,y의 평균 식을 이용해 정리하면 맨 오른쪽 항처럼 정리됩니다.
자! 이렇게 b1 유도 과정이 끝났습니다. b0은 y_bar에 대한 식에서 x의 평균값, y의 평균값, 유도한 b1값을 넣어주면 되겠죠?
지금까지 간단히 수학적으로 선형 회귀 모델을 푸는 방법을 알아보았습니다.
이제는 머신러닝 분야에서의 선형 회귀(Linear regression)을 알아보겠습니다.
머신러닝 분야에서는 위에 y-hat에 대한 식을 가설(Hypothesis), 즉 "x와 y의 관계는 이런 선형관계를 가질 것이다"으로 표현합니다.
따라서 아래와 같은 방정식으로 표현됩니다.

여기서 h는 Hypothesis를 뜻하고 theta는 parameters(또는 weights)를 뜻합니다.
위에 y-hat에 대한 식과 비슷하죠? b0는 Θ0과, b1는 Θ1과 매칭됩니다. 즉, 각각 절편(Intercept), 기울기(Slope)입니다.
그럼 Objective function을 생각해봅시다. 가설의 값과 실제 데이터의 값과 차이가 작아야 좋은 선형 회귀가 될 것 입니다.
그러면 'hΘ(x) - y', 위에서는 잔차(Residual)이라고 불린 것을 최소화 해주면 되겠죠?
여기서도 least-square의 개념이 들어갑니다.
아래와 같이 least-square형태로 만들어준 function을 'Cost function'이라고 부릅니다.

이 식도 위에서 본 Objective function과 형태가 매우 비슷합니다.
이제 Cost function을 최소화해주는 Θ0,Θ1을 머신러닝 모델을 통해 도출해내면 됩니다.
도출해내는 방법으로 우리는 경사하강법(Gradient descent method)를 사용합니다.
다음 컨텐츠에선 경사하강법과 Tensorflow를 이용한 Regression 구현에 대한 내용을 다룰 예정입니다.
지금까지 선형회귀(Linear regression)에 대해 알아보았습니다. 많은 도움이 되셨나요? 저희 앤트하우스와 함께 머신러닝의 기초를 단단히 잡아 봅시다:)
[머신러닝/딥러닝 시리즈]
#1 Introduction
http://blog.anthouse.co.kr/221098813480
#2 지도학습, 비지도 학습, 강화 학습
http://blog.naver.com/anthouse28/221098817606
차세대 주식투자 플랫폼, 알파스퀘어에서 스마트한 주식투자를 경험해보세요!
